[10000印刷√] y=x2乗のグラフ 976217-Y=x2乗のグラフの書き方

 #グラフ y=x^2 import matplotlibpyplot as plt import numpy as np x = np linspace (5, 5, 100, endpoint = True) #x座標の5〜5まで表示、配列の要素数、endpoint=True（終点を含む） y = x ** 2 y1 = x 3 plt plot (5, 5,0, 0, '', color = '#', lw = 1) #x軸 plt plot (0, 0,5, 25, '', color = '#', lw = 1) #y軸 plt plot (x, y, color = "red", linewidth = 25, linestyle = "", label = "y=x^2") #label=グラフY = a x 2 の関係にある2量に着目し、関数的な考え方を進んで活用しようとする 式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味定義：回転放物面 2変数関数 z = f (x,y) = x2 y2 の グラフ すなわち、 z = f (x,y) = x2 y2 を満たす (x, y, z) を全て集めた集合 { (x,y, z) z＝x2 y2 }

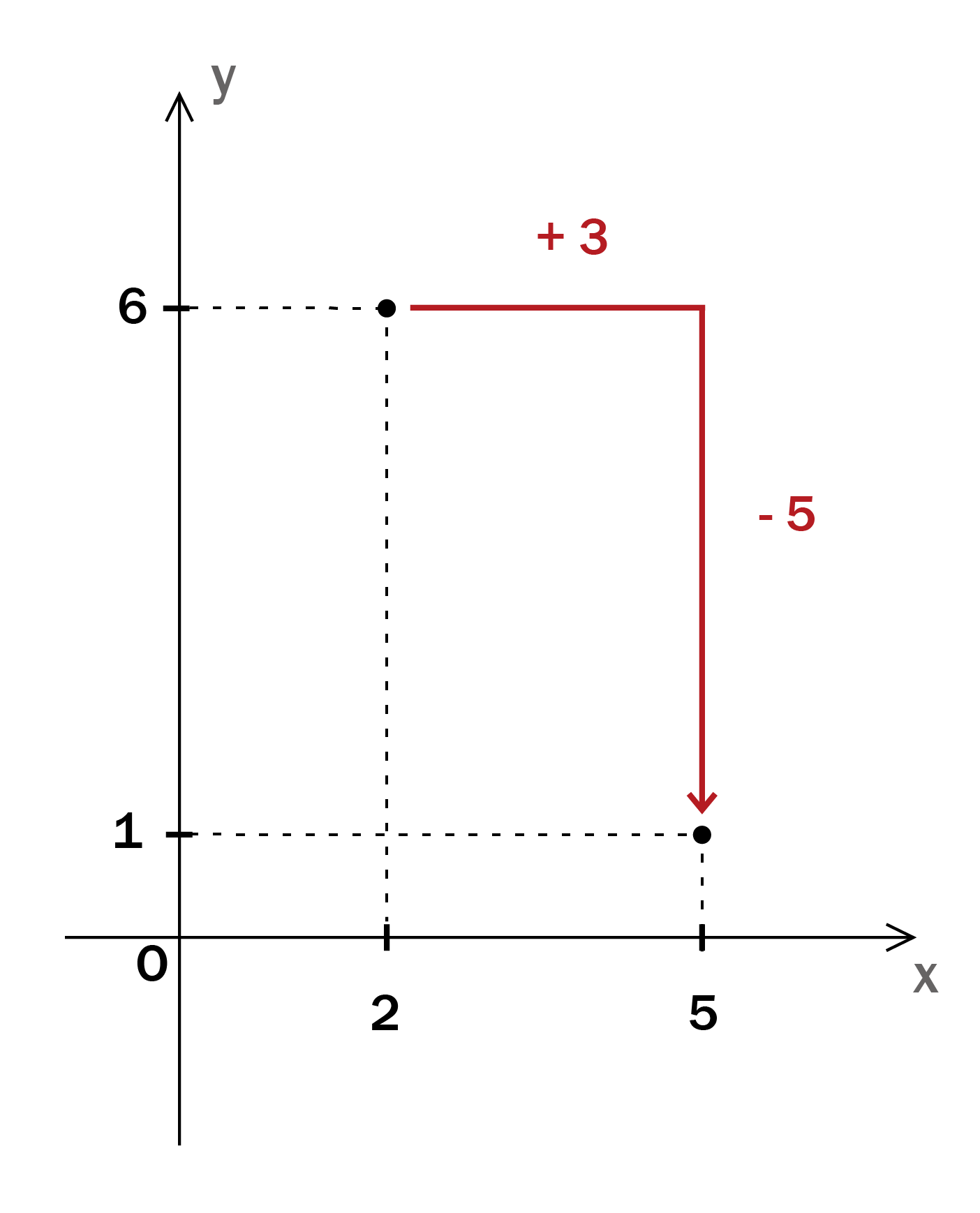
二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

Y=x2乗のグラフの書き方

Y=x2乗のグラフの書き方-Y=ax 2 のグラフの特徴 必ず原点を通り、その原点が頂点である。 y軸について対称である。 a > 0のときは上に開き、a < 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。 y=ax 2 のグラフとy=ax 2 のグラフはx軸について対象である。中3数学。2乗に比例する関数 (y ＝ ax²)。この a は「変化の割合」？ xの値が「0から2まで」増加する？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ 2次関数のコツ、成績アップ法を公開。

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

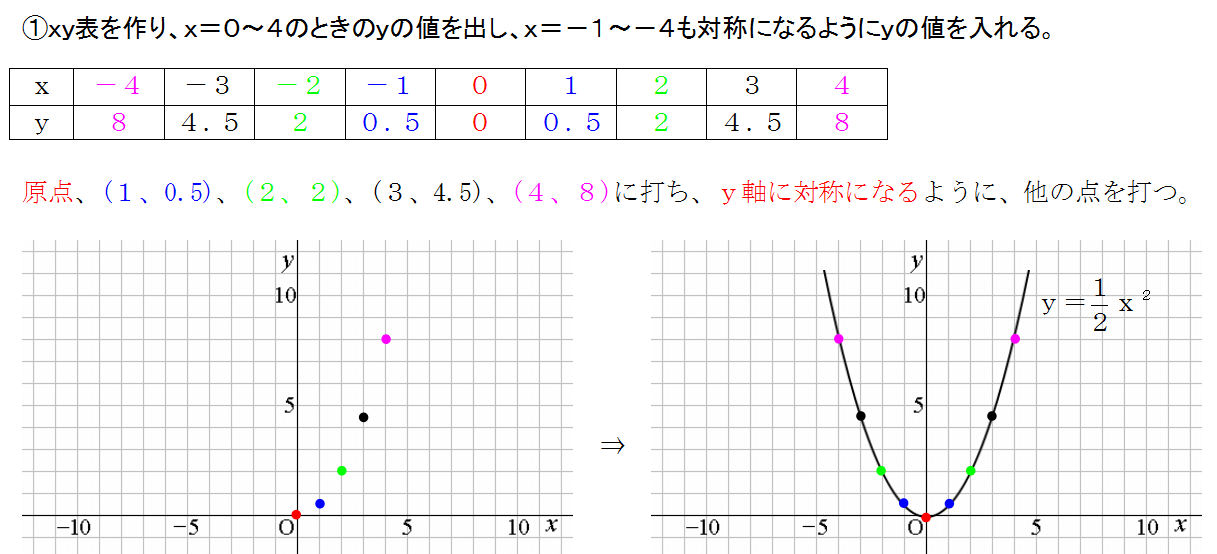
 媒介変数表示 グラフの概形 問題 x=cosθ,y=sin2θ（π2 2次関数の最も簡単な関数は y =x2 y = x 2 である．この関数についてグラフを考える． x x の値3，2，1，0，1，2，3に対する y y の値をを下の表に示す． 各 x x ， y y の組に対応する点を座標平面に描くと左下の図のようになる．表のような y = x2 y = x 2 のY = a x y 2 = a x y=\sqrt{ax}\iff y^2=ax y = a x y 2 = a x かつ y ≥ 0 y\geq 0 y ≥ 0 なので，グラフは放物線の一部になります（よく見る y = x 2 y=x^2 y = x 2 という放物線を 9 0 ∘ 90^{\circ} 9 0 ∘ 回転させたものの半分）。 b ≠ 0 b\neq 0 b = 0 の場合は平行移動すればよいだけです。

のグラフは, a>0 の場合、右図のようになります。 a>0の場合、xの正負にかかわらず、yは常に正の値をとっています。 また、y軸に対し左右対称であることも分かります。 そして座標平面において、1次関数が直線、反比例関数が双曲線を描くのに対し、 そうすれば、このようにグラフが完成します(^^) 分数がでてきて困ったときには 無視する！ これがポイントですね(^^) y＝ax2乗のグラフ書き方 まとめ お疲れ様でした！ 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ！ 中学数学二次関数y=ax2のグラフの書き方がわかる3つのステップ 二次関数y=ax2のグラフの書き方がわからない！ みんな、元気にしてる？そらだよ☆彡 今日は二次関数y = ax2 のグラフをかくんだ！ どちらかというと、今日は「絵を描く」感覚(^_)☆ え？

Y ＝ ax2 bx c＝のグラフ と変形することにより、軸が x = − b 2a で、頂点が (− b 2a, − b2 − 4ac 4a) の放物線となることがわかる。 グラフを描くときは、 y 軸との交点の y 座標（右のグラフの場合は c ）を書く習慣をつけよう。 これは、 x = 0 のときの y の y＝x 2 のグラフ（青色）も、y＝2x 2 のグラフ（緑色）も放物線になります。 比例定数が大きいほうがグラフは細長くなります。 なぜなら、x の値に対応する y の値が大きくなるからです。 放物線が y＝ax 2 で表されるとき、点（3，18）を通る放物線の式を求めてください。 1． y＝x 2 のグラフは、何軸に何対称ですか。 2． x 2 ＝16 の左辺と右辺を y と置きますY=x2乗1 グラフ Y=x2乗1 グラフY＝a（1－e^x）＋bといったときなど、式も計算できるとよい。 2 2224 男 / 歳未満 / 大学生 / 役に立った / 使用目的※ x 2 の係数 a で「形」が決まる． p ， q で「移動」が決まる． 例 y=2(x 3) 2 4 のグラフを書くときは，元の形として

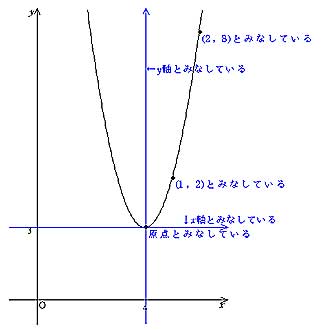
授業実践記録

二次関数のグラフ

 発展問題もアリ！ ｜中学数学・理科の学習まとめサイト！ y=ax2乗aの求め方についてパターン別に解説！ 発展問題もアリ！ を求めろって言われても 何をすればいいの！ ？ というわけで、今回の記事では中3で学習する関数 の単元から「 の求め 一般に、指数関数 y = ax y = a x について、 x = 0,1 x = 0, 1 のときに y = 1,a y = 1, a であることから、グラフは、 (0,1) ( 0, 1), (1,a) ( 1, a) の2点を通ることがわかります。 また、 x x が1増えれば y y は a a 倍に、1減れば 1 a 1 a 倍になることから、 a > 1 a > 1 ならグラフは文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R＝(－∞,∞） で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。

Aは正の定数とする 関数y X 2 4x 3 0 X A の最大値を求めよ 解き 高校 教えて Goo

二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

 二次関数 y ＝ x^2　（「２乗」をこう書きます）は「下に凸」なので、「頂点」で最小になります。 つまり「x=3 が頂点」ということです。Y＝x 2 のグラフと同じように、式を満たす x と y の値の組 を座標にとっていくと、点が隙間なくうまって下のよう な滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック！ y＝2x 2 のグラフの特徴 y軸に対して対称 下に凸グラフ y=1/4x^2 y = 1 4 x2 y = 1 4 x 2 1 4 1 4 と x2 x 2 を組み合わせます。 y = x2 4 y = x 2 4 与えられた放物線の性質を求めましょう。 タップしてもっと手順を表示する Rewrite the equation in vertex form タップしてもっと手順を表示する x 2 4 x 2 4 を平方完成します。

２乗に比例するグラフ 中学から数学だいすき

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

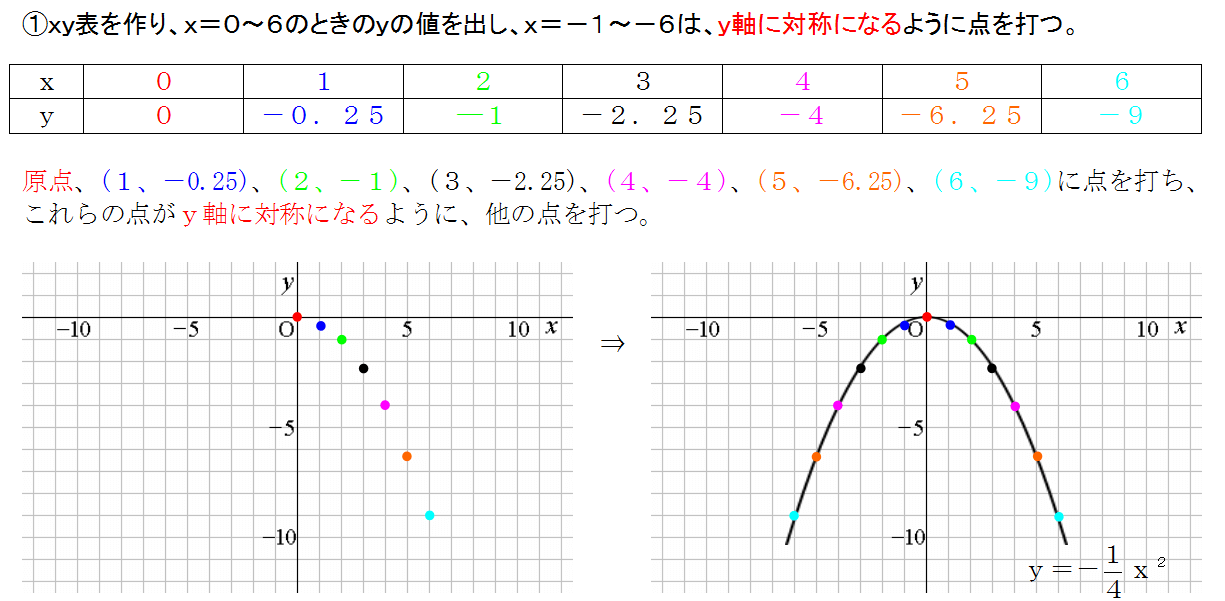
 そのため,\ 25 x25を描いたものとなっている それでもx=25付近ではx軸と一致してしまっているが,\ 実際にはy=0になることはない よって,\ 試験ではx軸と離して描いておくべきである ちなみに,\ この関数は標準正規分布の確率密度関数y={1}2πe^{\frac{x²}{2のカイ2乗分布（グラフ） 12 /2件 表示件数 5 10 30 50 100 0 1 1547 男 / 40歳代 / 教師・研究員 / 役に立った / 使用目的 自由度の大きさに応じてカイ自乗分布の形がどのように変化していくかを初学者に示す際に役立った 2 1627 女 / 50歳代 おわりに ここでは、二次関数 y = ax2 q y = a x 2 q のグラフについて見てきました。 このグラフのかき方は、次のようになります。 頂点 (0,q) ( 0, q) を把握し、座標を書く 頂点をもとに、放物線をかく 放物線上のどこか1点の座標を書く 放物線上のどこか

Y ｘ２乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋

Y X2とy X2のグラフを比べると これらはxに関してであ Yahoo 知恵袋

Y＝x 2 のグラフと同じように、式を満たすxとyの値の 組を座標にとっていくと、点が隙間なくうまって下のよ うな滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック！関数y=ax2乗放物線グラフの書き方はこれでバッチリ！ yはxの2乗に比例する関数 中3数学y＝ax2乗の変域の求め方を解説！Y＝x2乗＋5やy＝－(x－2)2乗など、平方完成できない式の最大値と最小値の求め方を教えてください ①平方完成 ②グラフ ③頂点、軸 写真にお願いしたいです🙏

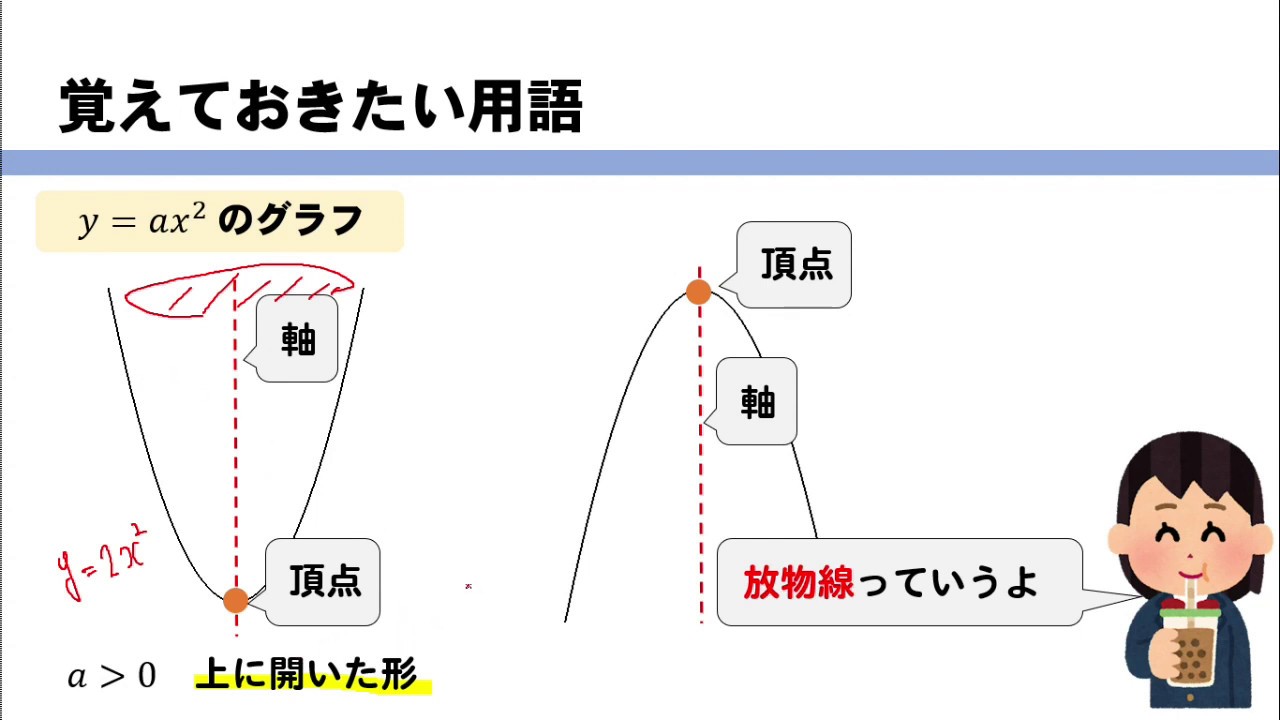
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

Y 1 X2乗のグラフ Youtube

そうすると，2次関数 y ＝ ax2 ＋ bx ＋ c のグラフと x 軸の共有点の x 座標は，2次方程式 ax2 ＋ bx ＋ c ＝0の解であることがわかりますね。 それでは，これで回答を終わります。 これからも，『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。2．3次関数（方程式）をグラフに描く グラフとは関数を満たす点の集合のことです。 グラフを描く時は、xとyの増減表を作れば簡単にできます。 それでは、y=x 3 の式をグラフに描いてみましょう。 まずは、y=x 3 の式のxとyの値の増減表を作ってみます。関数グラフ GeoGebra x y z π 7 8 9 ×

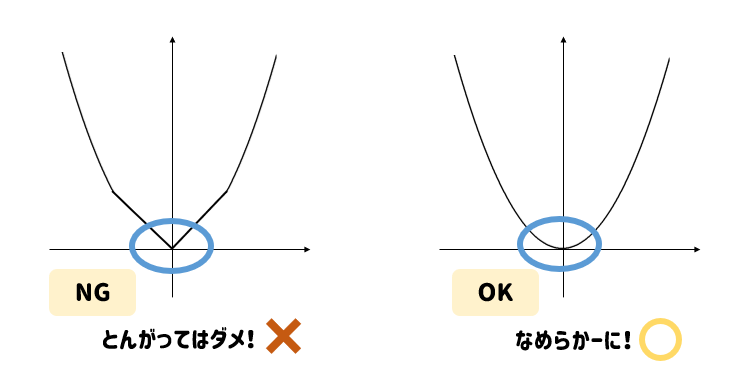
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋

2次関数 (3点→頂点) 2次関数の入試問題1 → ｽg ｽﾑ版は別包ｿｽ ｽ ｽ ｽi ｽ ｽ ｽﾎ費ｿｽj ｽQ ｽ ｽ ｽﾖ撰ｿｽ ｽﾌグ ｽ ｽ ｽt ｽm ｽW ｽ ｽ ｽ` ｽn → ｽ ｽ ｽ ｽpPDF ｽﾅは別包ｿｽ y= (x p) 2q ｽﾌグ ｽ ｽ ｽt ｽ ｽ y=x 2 ｽﾌグ ｽ ｽ ｽt ｽ ｽ x ｽグラフの縮小率： （0～1推奨） 指数関数のグラフ y=() 数式直接入力 y= x 25は、{x^2}5と書きます。 例：y={(1/2)^x}1（2分の1のx乗プラス1） 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。Y=ax 2 のグラフを，x 軸方向へ p，y 軸方向へ q だけ平行移動する。そこで，X=xp，Y=yq とおくと，x=Xp，y=Yq となるので，与式へ代入すると，Yq=a(Xp) 2 よって，

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

ｘ２乗 Y２乗 1を満たす実数x Yに対して 最大値と最小値を求めよ という問題なの Clear

Y = x 2という式をエクセルに渡しても理解しません 代わりに y = x 2という式を使った数値の表を作成して、それをグラフにします セル に 0 、セルB2 に=^2 と入力します。 キャレット ^は一般的な Windows キーボードの右上の方にあります、詳しくは → y=(x2)二乗1のグラフは、y=x二乗のグラフをx軸方向に(5 )y軸方向に(6 )だけ平行移動したものである。 その軸は直線(7 )頂点は(8 )(9 )である。 数学中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

２次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア

 今回は、y=x 2 8x15というグラフを例にとり解説します。 手順1：平方完成をする まずは平方完成をします。 y=x 2 8x15を平方完成すると、 y=(x4) 2 1となりますね。 手順2：頂点を求める y=(x4) 2 1より、 グラフの頂点の座標は(4,1) ですね。2次関数 y＝x2 のグラフと直線 y＝x＋2 とが交わっているとき，2交点A，Bと原点Oでできる OABの面積の求め方を考えてみます． 交点A，Bのx座標 は x2＝x＋2を解いて （→ x2－x－2＝0 → (x＋1) (x－2)＝0 ） x＝－1，2 直線ABがy軸と交わる点Pのy座標は y＝x＋2 から y＝2 ここで， OPBの面積は，底辺の長さ2，高さ2と考えると S1＝2×2÷2＝2です． また， OPAの面積 は，底辺の長

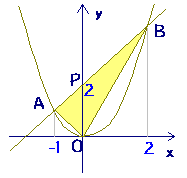
2次関数のグラフと直線

基本 指数関数のグラフ なかけんの数学ノート

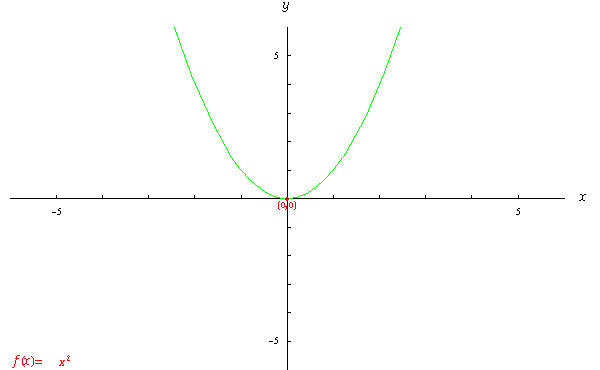
1変数関数y F X X 2の性質 数学についてのwebノート

ガウス記号 ２ Y X 2 のグラフを書こう 身勝手な主張

関数です Y X２乗のグラフ上の３点a B Cのx座標がそれぞれ Yahoo 知恵袋

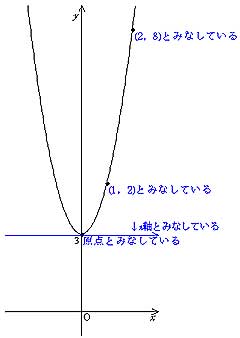
授業実践記録

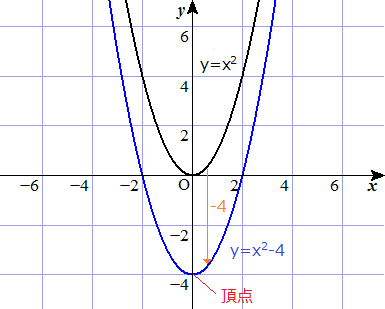
例題で学ぶ高校数学 Y Ax2 Q

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

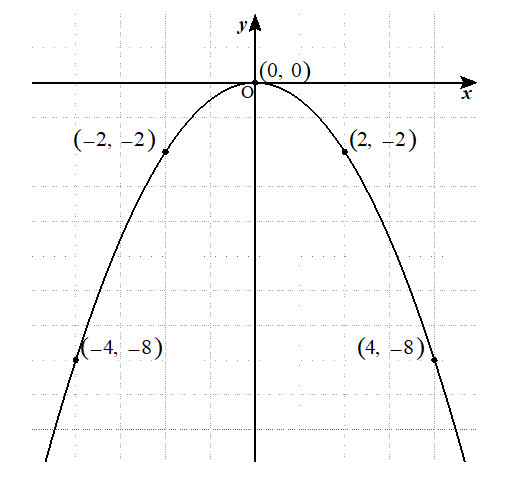
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット

４乗のグラフ ２乗のグラフは学校で習いました ４乗のグラフはどんな 数学 教えて Goo

Y X2乗 2 X のグラフの式を教えてください 2乗は 2 Yahoo 知恵袋

指数方程式

とまて週報 二次関数で語れ１

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube

例題で学ぶ高校数学 Y Ax2 Q

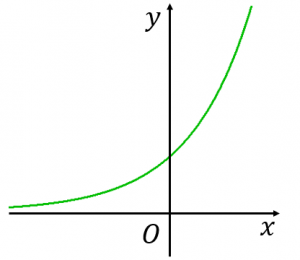
Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学

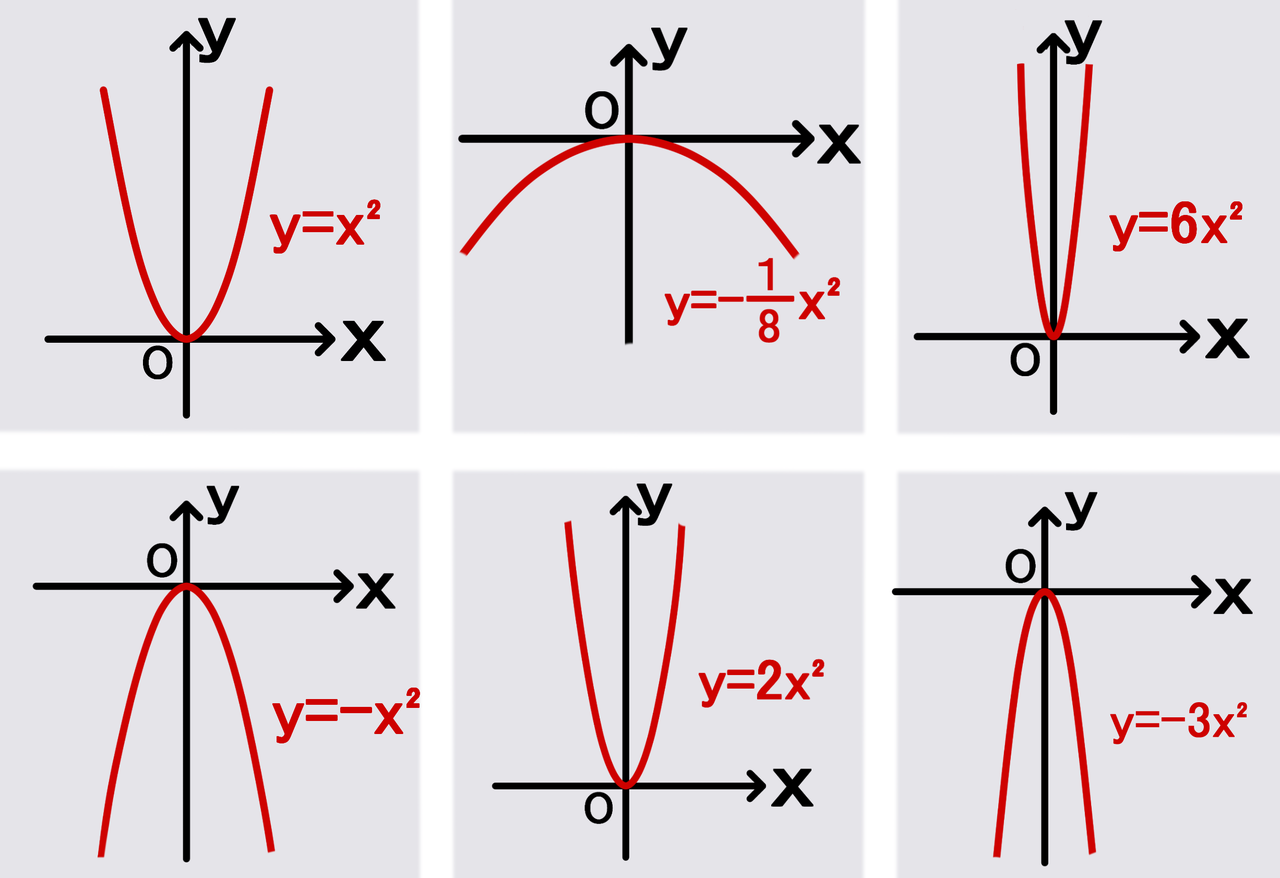
2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

Y 1 X ２乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

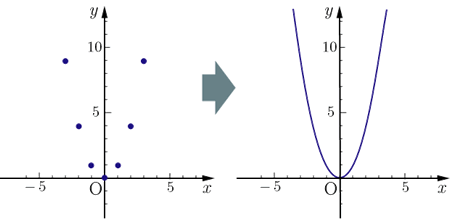
2次関数のグラフ Y X 2

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

Y 1 2x 2 二分の一エックスの二乗 のグラフを書いてみたのですが これでいいの Clear

二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

Y 1 X ２乗 のグラフってどんなんですか 大体でいいので教えてください Clear

最も人気のある Y X2乗 グラフ シモネタ

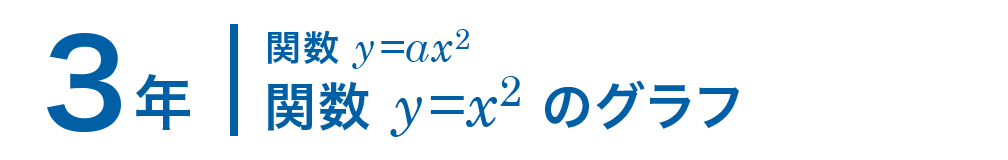
3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

ｙ ｘ２乗 2ｘ 2を平方完成したらどうなりますか 途中式教えてください Clear

1

関数ｙ ｘ２乗のグラフである は直線である Pqのエックスの座 Yahoo 知恵袋

２次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア

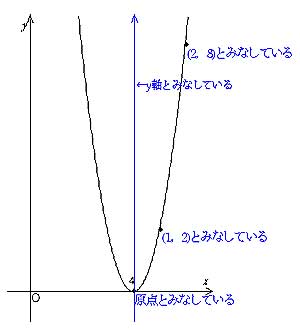
授業実践記録

二次関数のグラフ

Mathematics 関数と証明 大阪府公立 ２２年前期理数科 働きアリ

数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo

この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave

二次関数y X 2 2のグラフです黄色の線は何を求めてるんですか Yahoo 知恵袋

数学1二次関数のグラフで Y ｘ二乗 1のグラフの書き方がわかりません Yahoo 知恵袋

数学 中3 35 二次関数のグラフ Youtube

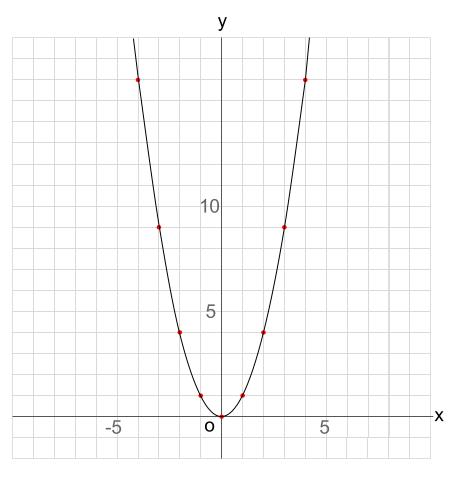
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート

２次関数のグラフ

2次関数の問題で Y X２乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋

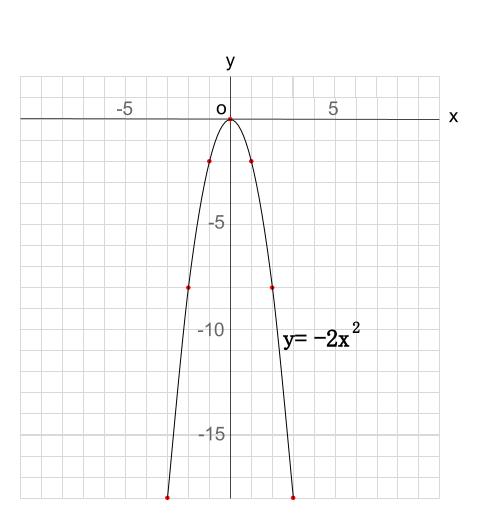
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

２乗に比例するグラフ 中学から数学だいすき

中３ ２次関数

Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

1

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

解説がわかりません なぜｙ ｘ２乗 3ｘを平行移動した放物線の二次関数はｙ ｘ２乗 Clear

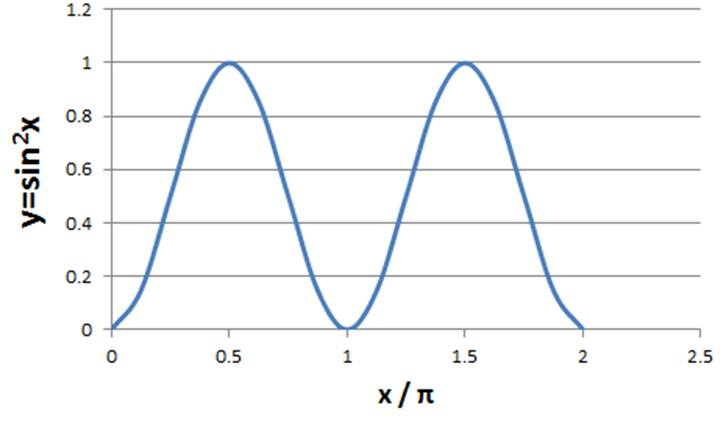
Y Sin 2x のグラフや周期は Y Sin 2 8を微分するとどうなるのか ウルトラフリーダム

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

２次関数のグラフと直線

1

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

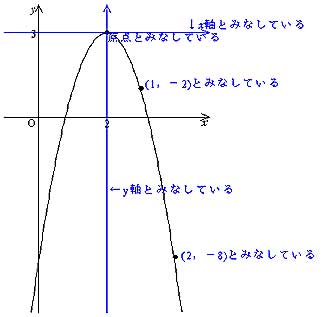
授業実践記録

2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題

2乗に比例する関数 グラフ

中3数学 Y X2乗のグラフ 5分で学習 Youtube

Aは正の定数とする Clear

関数y X 2のグラフの性質 勉強ナビゲーター

中3数学 Y X2乗のグラフの変域 5分で学習 Youtube

Y X二乗 2 Xのグラフの書き方がわかりません 教 Yahoo 知恵袋

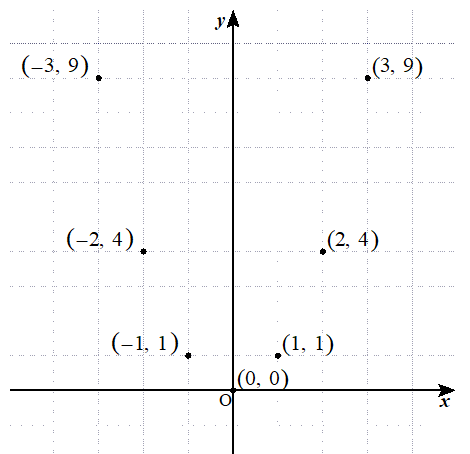
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ

数式のグラフ

3

Y 1 X2乗のグラフ Youtube

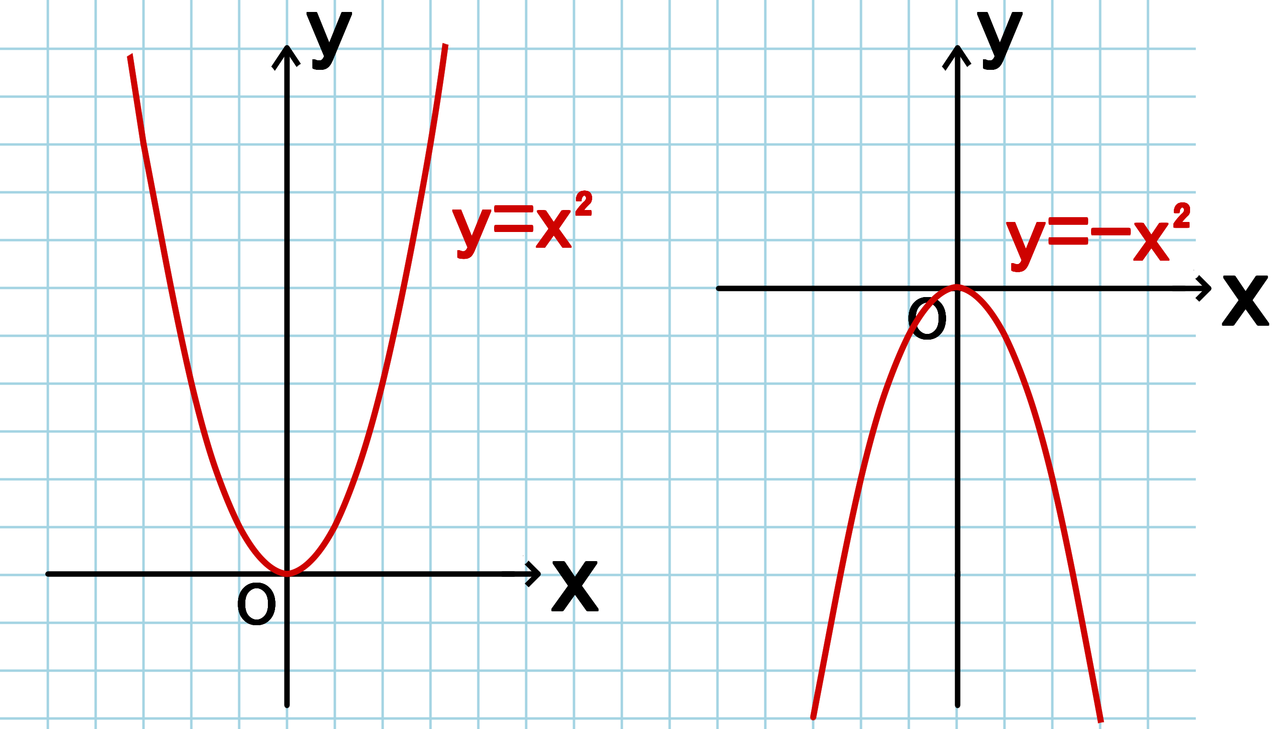
2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学

二次関数の値の変化 Y X2 4x 5を 平方完成してグラフを書く 私 Yahoo 知恵袋

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

数学で 右の図のように 関数y ｘ２乗のグラフ上にx座標が Yahoo 知恵袋

Y 3分の1ｘ2乗 2ｘのグラフの ｘ切片の求め方を教えて下さい Y 0のときの途中 Clear

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

因数分解とグラフ 中学から数学だいすき

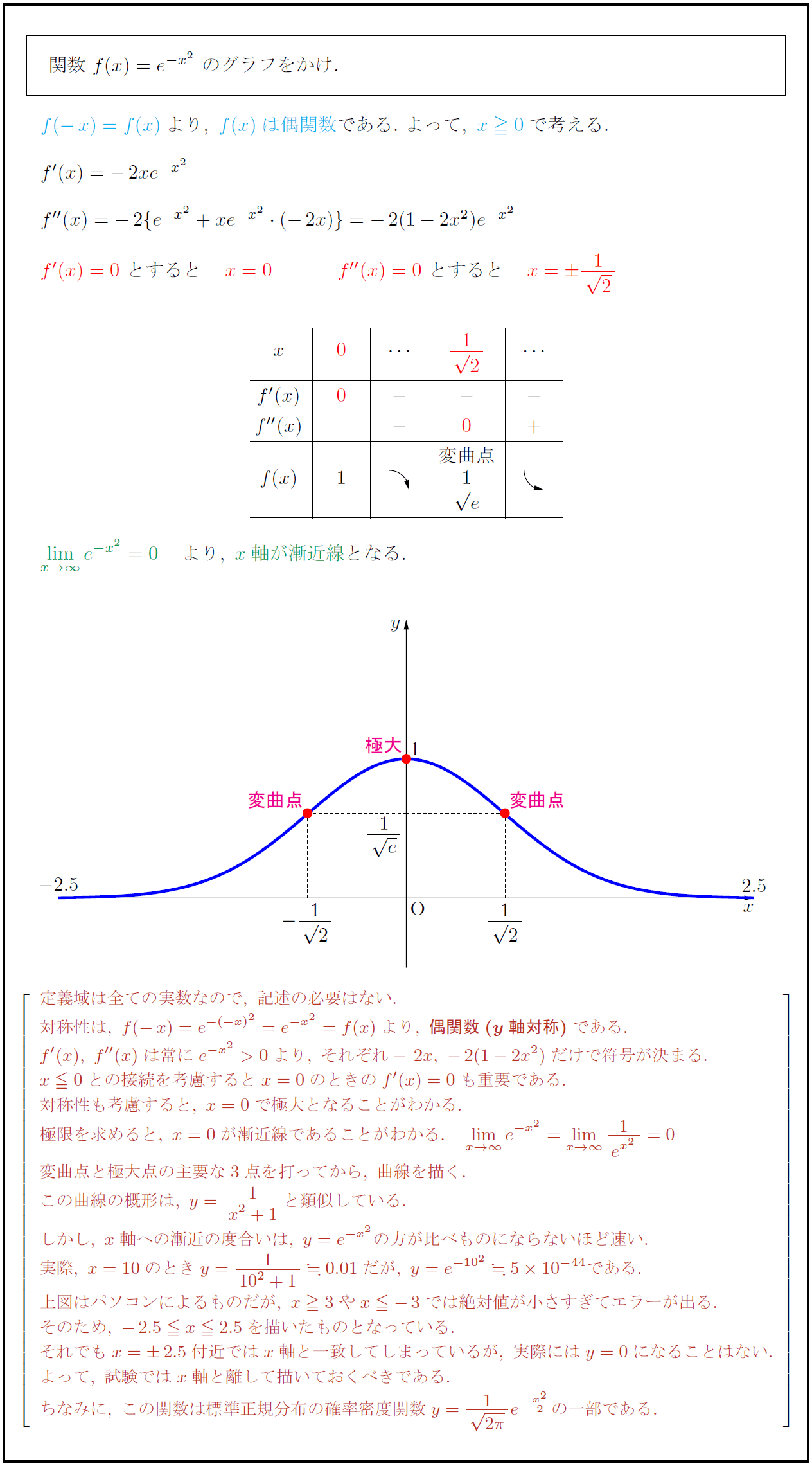
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月

Incoming Term: y=x2乗のグラフ, y=x2乗のグラフの書き方,