今日は、先週の予告通りに、四角形の分類と性質についてです。 まず、四角形とは、4本の辺で囲まれた図形のことですね。 しかし、一言で四角形と言っても、いろいろな形の四角形がありますね。 算数で主に扱う四角形は次のように分類することができます。 ①台形:向かい合う1組の辺== 四角形の性質 == 《問題》 次の各性質がつねに成り立つ図形に を付けなさい. (※この問題では,成り立つものはすべて ,成り立たないものはすべて としたときだけが正答となり,1つでも間違っていると正答とはなりません.各々6個のチェックボックスが完全に合っていなければ正答とは交わる四角形は、平行四辺形 二等辺三角形の頂角の二等分線は, 底辺を垂直に2 等分する さが等しい 1組の対辺が平行でその長 四角形は、平行四辺形 2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形
Www N It Its Jp Uploads B240ddfcba4b17c9d0864e4395bf6b66c9 Pdf
図形 の 性質 四角形
図形 の 性質 四角形-・性質 (対角線をのぞく) ①4つの角が等しく、4つの辺が等しい (定義)四角形の性質 4本の直線、これを辺という。この辺に囲まれた図形を四角形といいます。 直線と直線が交わった点を頂点、頂点と頂点を結ぶ線を対角線という。 長方形って、何? ①4つの角が全て直角になっている四角形。




条件は長方形 ひし形 正方形 全部当てはまってるから3つじゃないんですか なんでひし Clear
2組の対辺がそれぞれ平行な四角形を平行四辺形と言う。 平行四辺形の性質 ① 平行四辺形の2組の対辺はそれぞれ等しい。 ② 平行四辺形の2組の対角はそれぞれ等しい。 ③ 平行四辺形の対角線はそれぞれの中点で交わる。 平行四辺形になる条件 ① 2組の対辺がそれぞれ平行である。 ② 2組のした四角形の性質や平行四辺形になるための条件 などを復習する。また証明において,結論を導く ために何を根拠にすべきか明確にし,生徒に見通 しを持たせている。本時では動的ソフト GeoGebra¹⁾を用いて図形を連続的に変形させ, 既習事項を活用する活動を行う。授業内容として は四角形の性質 長方形の対角線は、長さが等しい。 ひし形の対角線は、直角に交わる。 正方形の対角線は、長さが等し、垂直に交わる。 スポンサーリンク 希望屋 関連記事 中2数学さいころの確率の解き方と練習問題 確率の中でも、「さいころ」の確率についての
図形の性質と証明⑨いろいろな四角形A 学 年 2年 学習日: 月 日( ) 中学校数学・ワークブック 中学校数学 2B5 -9A 年 組 氏名 〔 Point〕いろいろな四角形 台形の定義 1組の対辺が平行である四角形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 長方形の定義 4つの角が平行四辺形の対角線は(それぞれの中点 )で交わる。 4 次の問いに答えなさい。 (1)ひし形,長方形,正方形について,それぞれの定義と対角線についての性質を書け。 ひし形 (定義) 4つの辺が等しい四角形 (性質) 対角線は垂直に交わる。円に外接する四角形の性質を理解するための前提知識です。 円外の点 a a a から引いた2本の接線の接点を p, q p,q p, q とするとき a p = a q ap=aq a p = a q 証明 円の中心を o o o とする。 円の半径より o p = o q op=oq op = oq;
三角形の内角の性質 三角形の内側にある角のことを 内角 といい、 すべて足すと180°EC = BE ×E D四角形 四角形の定義 4つの線分で囲まれた図形 四角形といいます。 向かい合う辺を対辺といいます。 対辺 辺abと辺cd 辺adと辺bc 向かい合う角を対角という。




高校数学 円に内接する四角形の対角線の長さと面積 受験の月
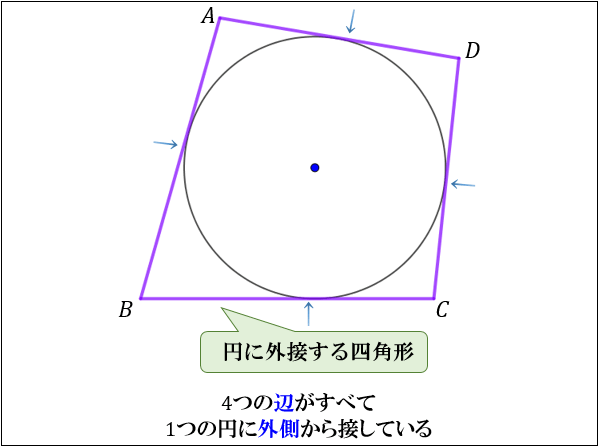



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ
すべての四角形の内角の和は360° になります。 三角形、四角形の外角を知り、外角の和が 360°を確認する △ ABC の外側にあるので ∠Cの外角 といいます。平行な四角形 性質1 2組の対辺は それぞれ等しい 性質2 2組の対角は それぞれ等しい 性質3 対角線はそれぞれの 中点で交わる。 印刷して、紙の上でやってネ! 印刷用 1 上の定義を,記号で表しなさい。 ab ad 2 上の性質1を,記号で表しなさい。 ab ad 3 上の性質2を,記号で表しなさい。 ∠a四角形の性質の探求 ~図形の性質の発見ツールとしてのCABRIⅡの利用例~ 上原永護(群馬県前橋市桂萱中学校) EMAILmow@mailwindnejp 1.はじめに 中学2年の図形の学習では、三 角形や四角形、相似な図形の性質 について学習する。その学習内容 と関連する問題に、四角形の4つ の辺の中点を
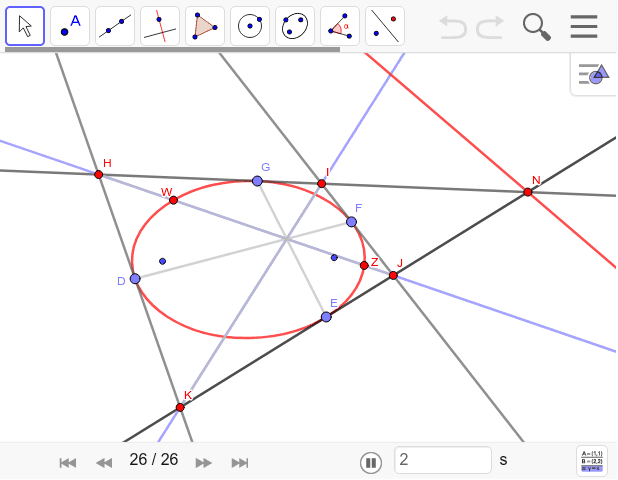



楕円に外接する四角形の性質 Geogebra



Www N It Its Jp Uploads B240ddfcba4b17c9d0864e4395bf6b66c9 Pdf
一方で定理は定義から導かれる性質です。 平行四辺形は3つの特別な性質がありますが、これらは「四角形の向かい合う2組の辺がそれぞれ平行」ということに由来するものです。 では平行四辺形の性質を定義から証明してみましょう。 平行四辺形の性質の証明組の対辺がそれぞれ平行な四角形を平行四辺形という。 ab ™ dc , ad ™ bc 2 平行四辺形の性質 平行四辺形には,次のような性質がある。 まずは,四角形の"対辺"と"対角"の意味を説明しておきましょう。四角形の向かい合う辺を 対辺 ,向かい 合う角を対角といいます。 次に,2の性質が1 単元名 垂直・平行と四角形「四角形をつくろう」 2 単元とその指導について (1) 教材観 本単元では,以下の3点をねらいとしている。 ① 垂直,平行や台形,平行四辺形,ひし形の性質について調




条件は長方形 ひし形 正方形 全部当てはまってるから3つじゃないんですか なんでひし Clear




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
「円に内接する四角形の性質」ではありませんが,円周上に4点がある場合方べきの定理を使うことが多いです。 性質4 (方べきの定理) AE\times EC=BE\times ED AE ×図形 定義 性質 三角形 3本の直線で囲まれた図形 角が3つある。 角の総和は180°である。 四角形 4本の直線で囲まれた図形 角が4つある。 角の総和は360°である。 対角線が2本ある。 長方形 すべての角が直角の四角形 向かい合う辺が平行である。台 形 : 平行が一組ある四角形 ひし形 : 平行が2組で、4つの辺の長さが等しい四角形 ここで面白かったのが〈ひし形〉で「先生、顔を横にすれば平行四辺形だよ」という声があった。



中3数学 円の性質11 四角形が円に内接するための条件 すべて無料 星組の中学数学講座




特別な四角形 無料で使える中学学習プリント
4 四角形の面積 公式のまとめ 1 四角形の種類と性質 四角形には、台形、平行四辺形、長方形、ひし形、正方形など、いろいろな形のものがあります。 台形は、向かい合う1組の辺が平行という条件だけを満たすものですが、平行四辺形になると四角形の種類と定義 四角形が 「4本の直線で囲まれた平面上の図形」 と定義されますが、正方形や長方形などの特殊な四角形はそれぞれ次のように定義されます。接線より ∠ a p o = ∠ a q o = 9 0 ∘ \angle apo=\angle aqo=90^{\circ} ∠ a po = ∠ a qo = 9 0 ∘;



学校や塾であまり教えないが 受験に必要な知識 3 四角形の分類 中学受験 算数 虎の巻 東京 駒込 進学塾サクセス 塾長ブログ



Http Www City Kofu Yamanashi Jp Gakkoukyoiku Gakusui H Jisyuuprint Suugaku Jp Suugaku06 Pdf
三角形の垂心がもつ性質の証明をします。 まずは「 四角形ADHF,BEHD,CFHEは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。 四角形CFHEに注目すると、\(\angle CFH=90^\circ\),\(\angle CEH=90^\circ\) したがって、円周角の定理のひし形の性質 性質①2 本の対角線は垂直に交わる 性質②2 本の対角線は、互いにほかを 2 等分する 性質③1 本の対角線は、ひし形を合同な 2 つの二等辺三角形に分ける 性質④2 本の対角線は、ひし形を合同な 2 つの直角三角形に分ける円に内接する四角形の性質まとめ対角の和が180°になる理由 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
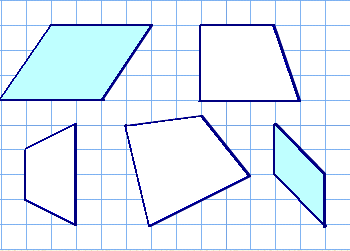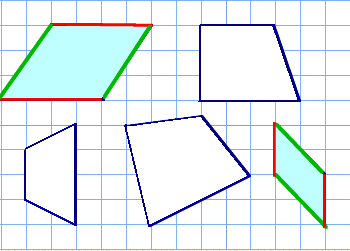



4年算数 垂直 平行と四角形 2 教え方
三角形・四角形 平行四辺形の性質 平行四辺形 平行四辺形2組の対辺がそれぞれ平行な四角形(定義) 平行四辺形の性質 定理 平行四辺形では ①2組の対辺はそれぞれ等しい。 ②2組の対角はそれぞれ等しい。 ③2つの対角線はそれぞれの中点で交わる。 1x、∠yの大きさと、m、nの長さを求め2 GeoGebraを使って,円に内接する四角形の性質を予想する。 T1:点を動かすと四角形の形が変わりますね。どの四角形についても,成り立ちそうなことはありますか。 S1:向かい合う角の大きさを足すと180°です。 S2:(対角線を結んだとき)向かい合う三角形は相似です。 S3:(対角線の交点をになります。 これは小学生のときに学習しているので覚えている方も多いでしょう。 でも じゃぁ、何で180°になるのか知っていますか? と言ったら、困ってしまい




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
三角形や四角形の性質を利用して,身近なことがらを調べること 5章をふり返ろう 1 力をのばそう (-) 活用・探究 折り紙の不思議な性質 (-) 社会にリンク パズル作家 北村良子さん (-) 6章 データの比較と箱ひげ図 〔5〕 1節 箱ひげ図 (3) 1 四分位数と四分位範囲 1 四分位数,四分位範囲




平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




中学校数学 証明のコツ 四角形の性質




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
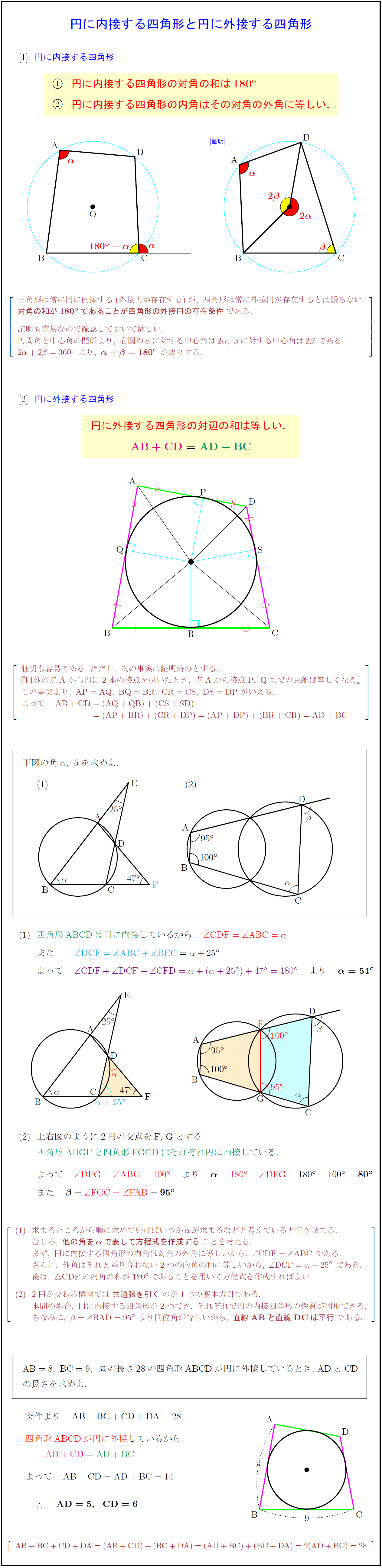



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月



図形の扉 四角形の性質




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




算数 小四レベル 四角形の性質 算数 四角形の性質




中学校数学 証明のコツ 四角形の性質



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



しょうちゃん 公式ブログ 四角形の性質 Powered By Line



図形の扉 四角形の性質




長方形とひし形 セルモ大蔵 世田谷 の塾長ブログ



5年生 四角形の性質を調べよう 高岡市立福岡小学校



1



算数tips 算数の効率的な学習 その5
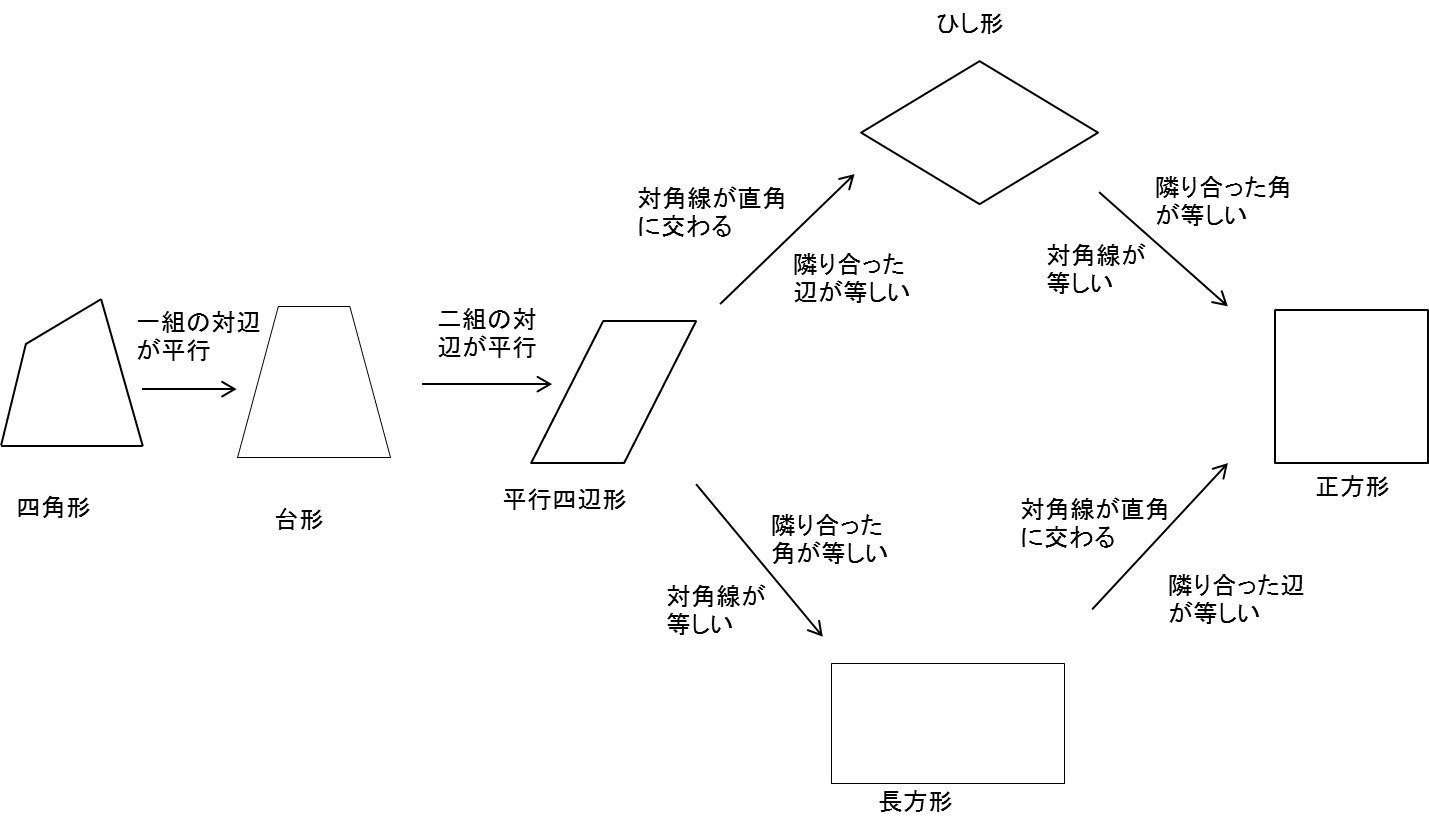



140字で高校受験 数学 四角形の性質まとめ 四角形 台形 平行四辺形 長方形 ひし形 正方形 高校受験 数学 Http T Co Tumufb1q86



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



1
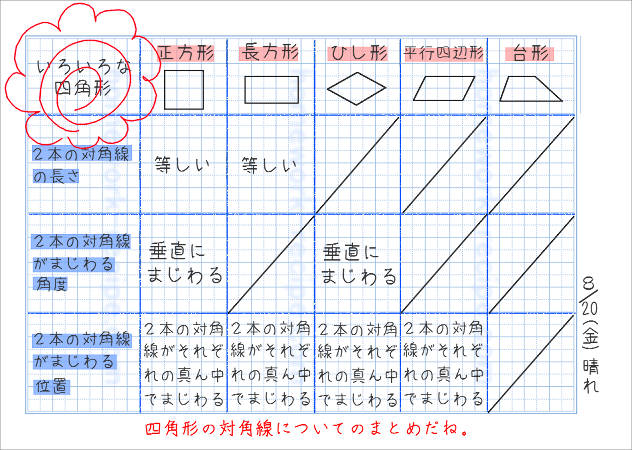



いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ



Www Pref Hiroshima Lg Jp Uploaded Attachment 1195 Pdf




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中学校数学 証明のコツ 四角形の性質



四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究
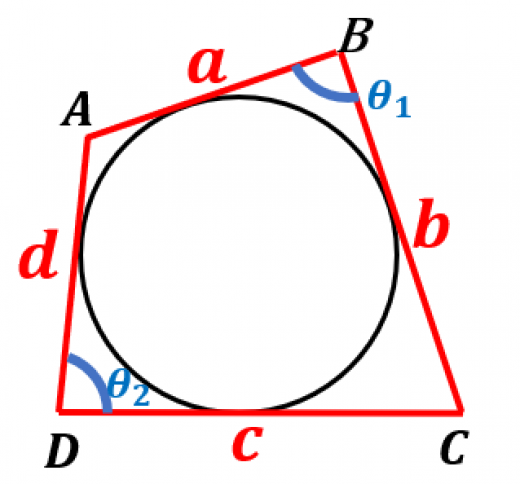



円に外接する四角形の重要な2つの性質 高校数学の美しい物語



中2数学 長方形 ひし形 正方形のまとめ おっくうの教材作成日記 楽天ブログ




算数 小4 19 四角形の特ちょう Youtube



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張
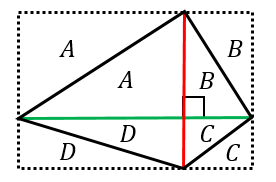



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学




いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ 学習 学習ノート 子供の教育




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



四角形 12時目



3




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
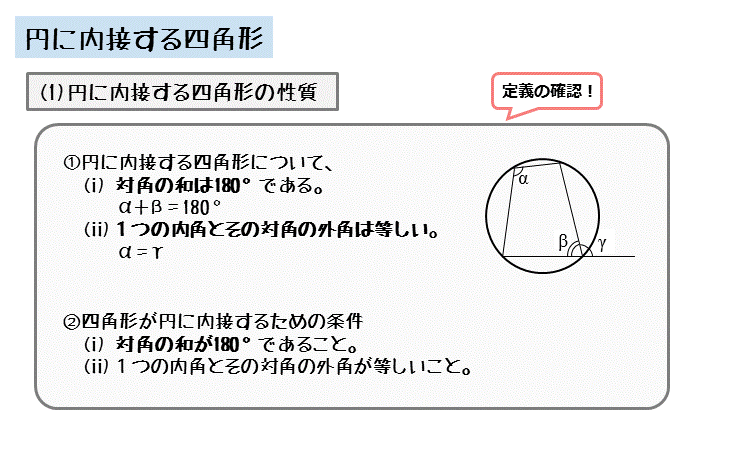



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん
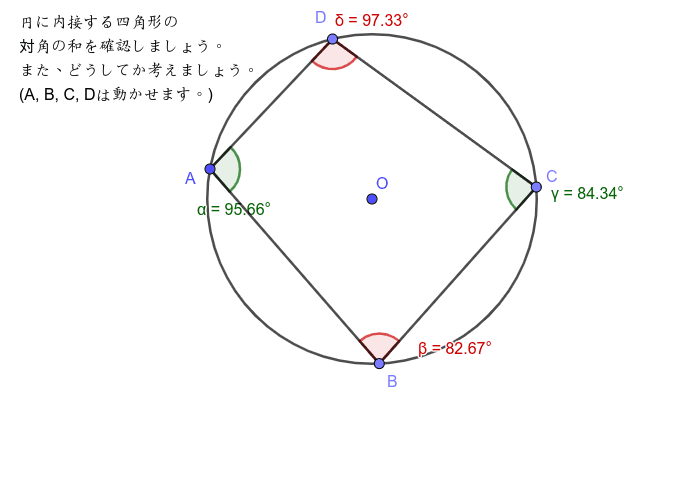



円に内接する四角形の性質 Geogebra
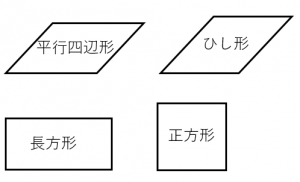



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
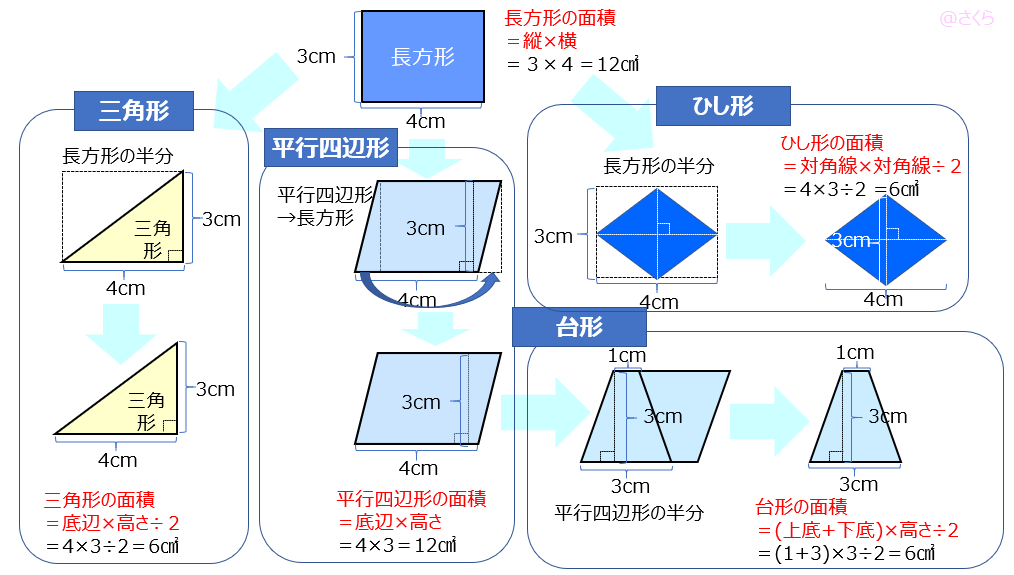



四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦




いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ
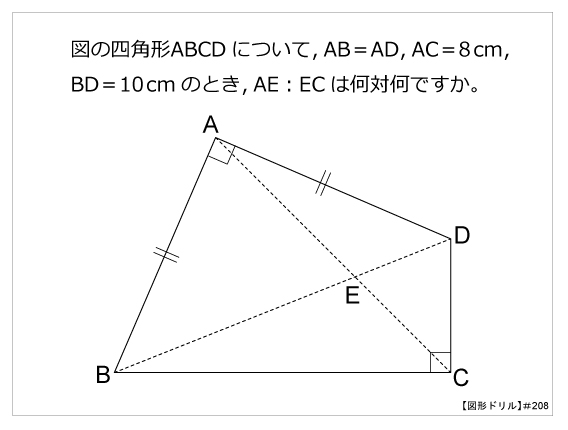



図形ドリル 第8問 四角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく



Http Www Edu C Pref Aomori Jp Action Common Download Main Upload Id



Http Sansutp Com A12 14 Pdf




対角線の学習 ますます算数



小6算数 多角形と対称 指導アイデア みんなの教育技術
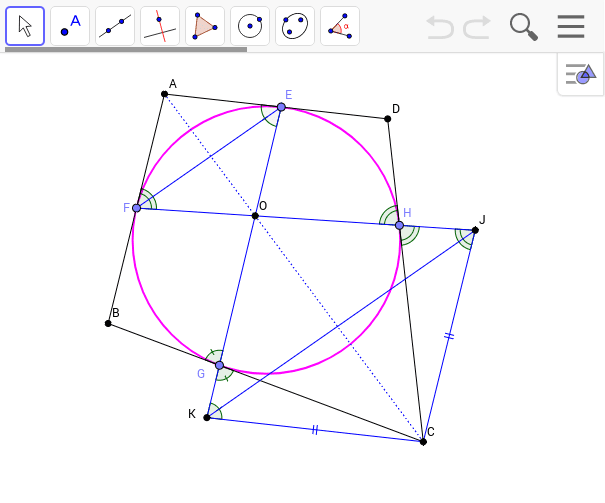



外接四角形の対角線の証明 Geogebra
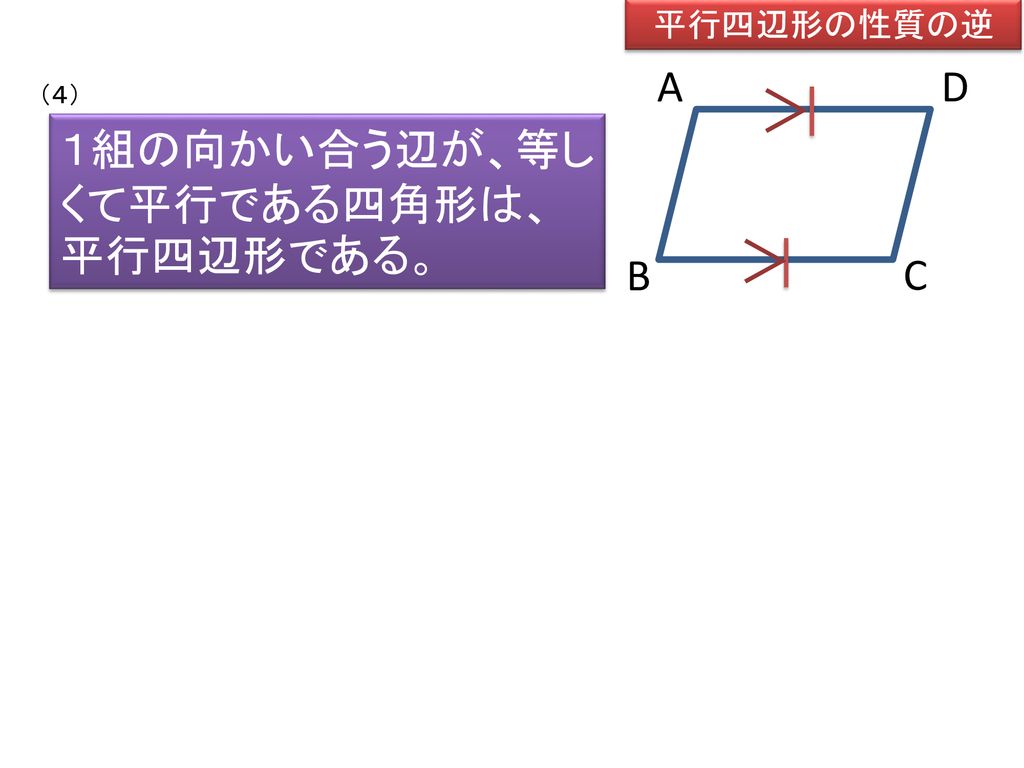



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download



4年算数 垂直 平行と四角形 2 教え方




小学4年生 算数 7月 ひし形の性質 四角形の対角線 整数のわり算 3 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



図形 色々な四角形の性質 要点note



1
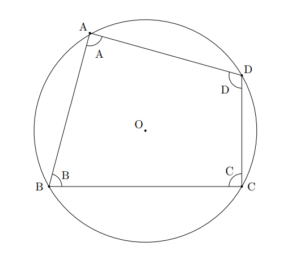



円に内接する四角形の性質 高校数学の知識庫




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



図形の扉 四角形の性質
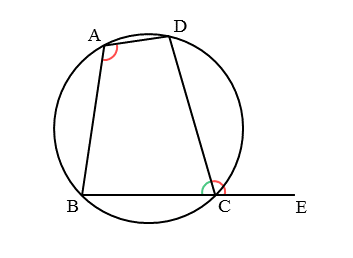



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん




Sinb0 Sinbsqrt1 Cos2bsqr Descubre Como Resolverlo En Qanda
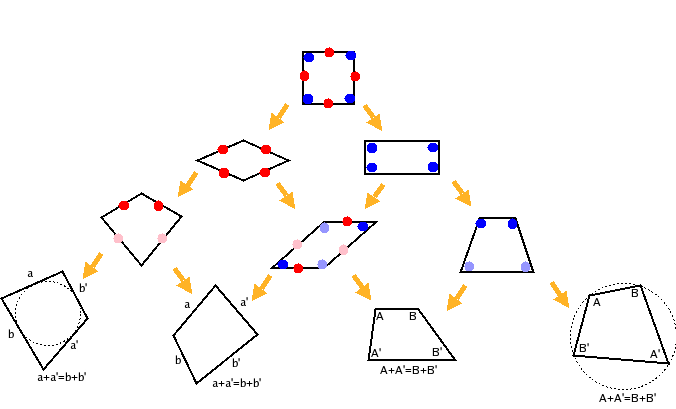



四角形の分類 低次元日記
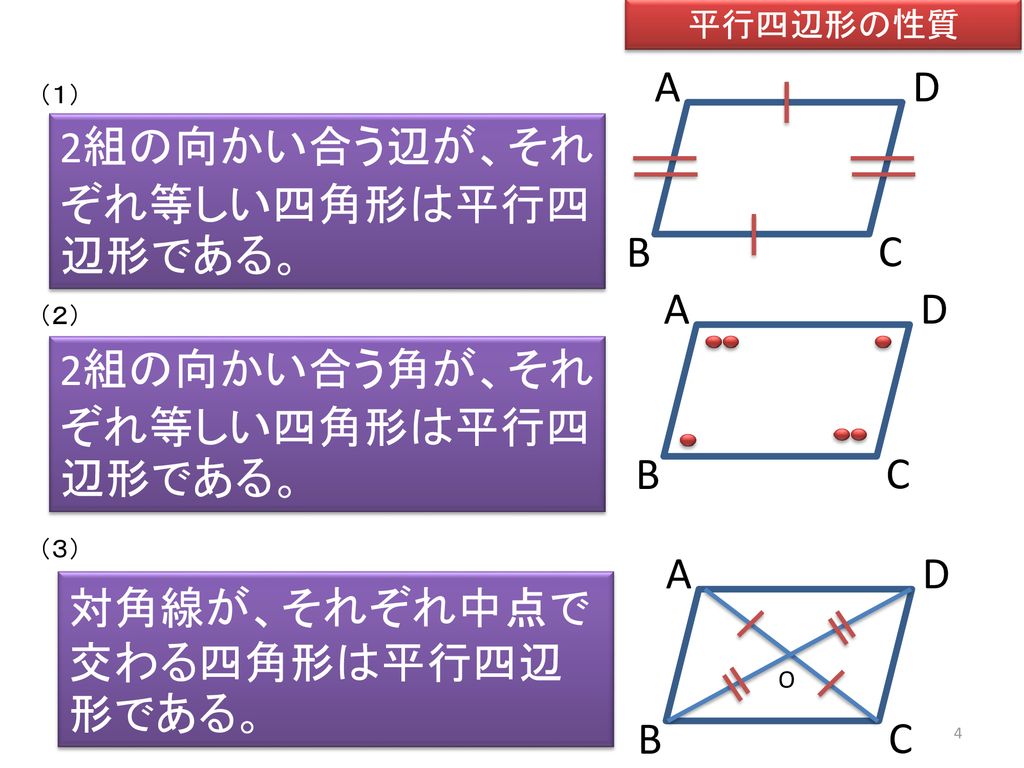



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




高校 数学a 図形24 円に内接する四角形 8分 Youtube
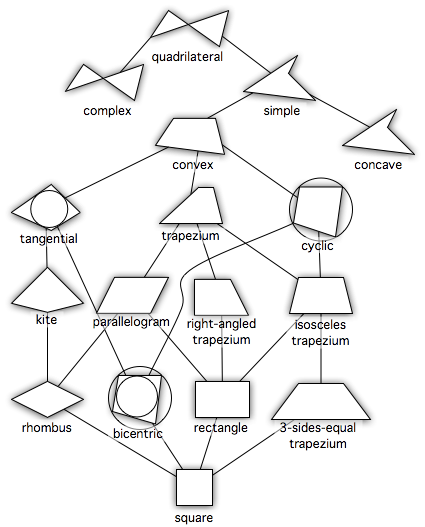



四角形 Wikipedia
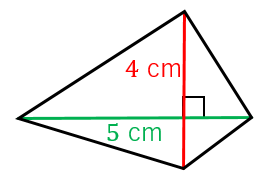



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



対角線で参観 教育考現学
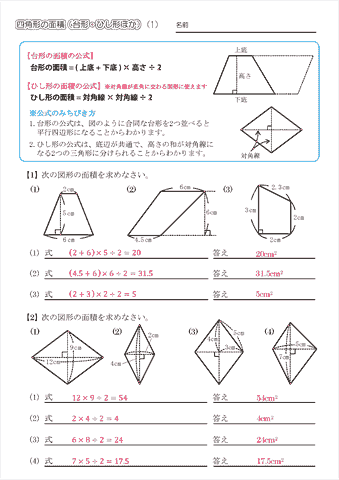



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
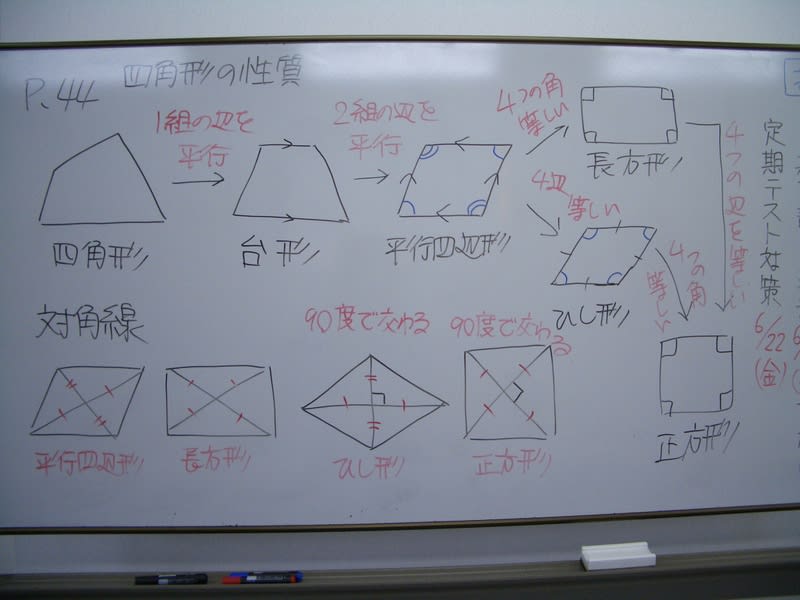



小5算数 四角形の性質 ブログ アビット
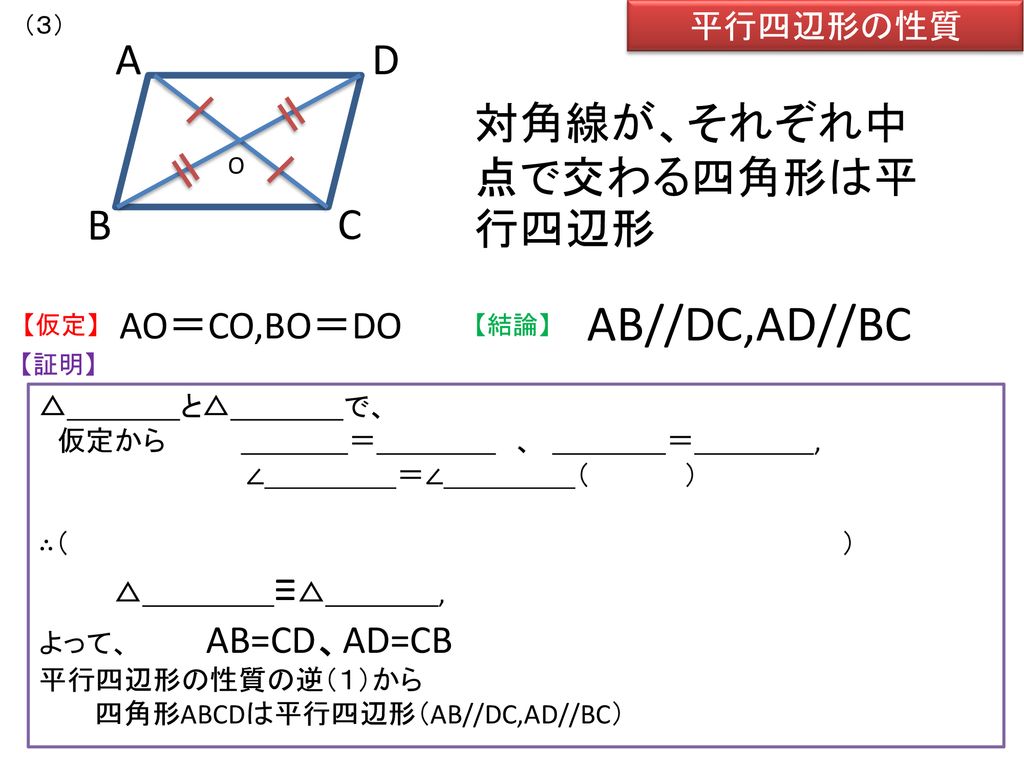



平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch



みんなの算数オンライン 中学受験 4年 四角形の性質と分類 四角形の性質と分類 例題と解説




四角形の性質と証明 無料で使える中学学習プリント



この四角形の面積の求め方を教えてください 難しいことを考えず普通に考 Yahoo 知恵袋
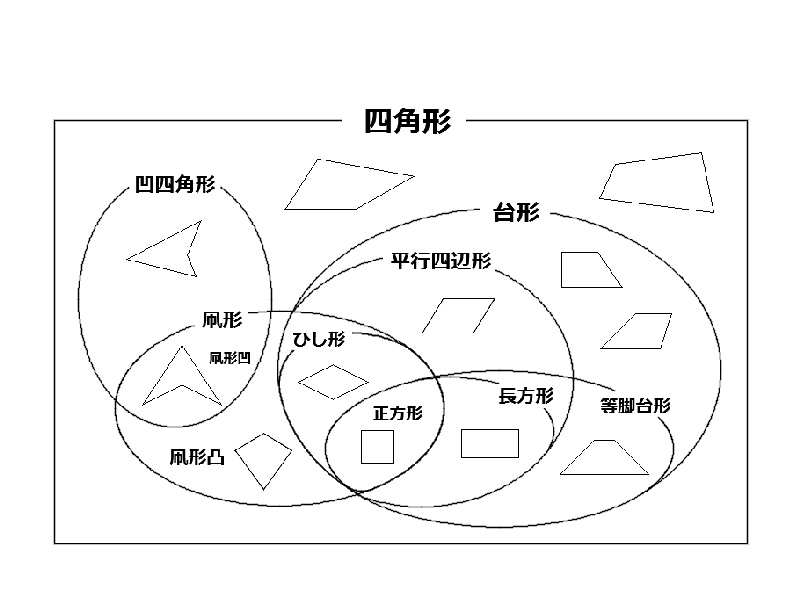



数学 四角形 この世界の勉強記録



Studydoctor円に内接する四角形の性質 中学3年数学 Studydoctor



学校や塾であまり教えないが 受験に必要な知識 3 四角形の分類 中学受験 算数 虎の巻 東京 駒込 進学塾サクセス 塾長ブログ



Http Www1 Center Spec Ed Jp D H18 H18 Da08 Sansuu Suugaku Pdf Zukei Zukei 3 Pdf



四角形 Wikipedia
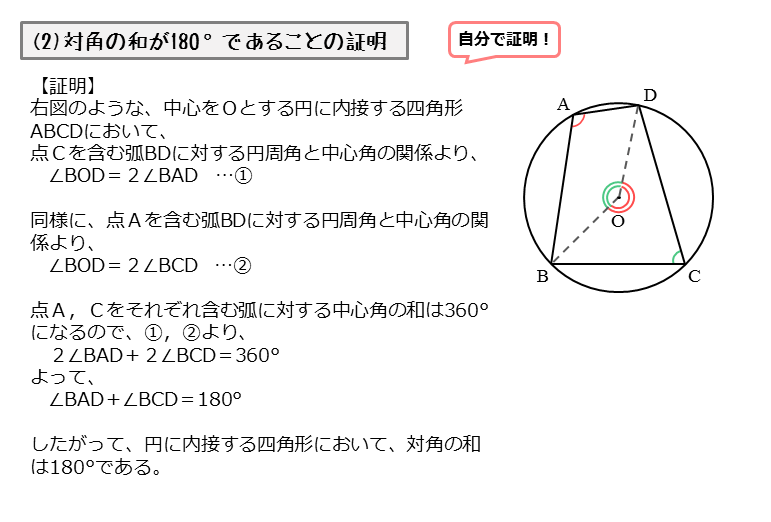



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



48s96ub7b0z5f Net Naisetsu Shikakukei




いろいろな四角形について 小3 小4 小5 小6 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生




この問題 答えだと2枚目の写真のような感じになっているのですが 私は対角線がそれぞれ Clear
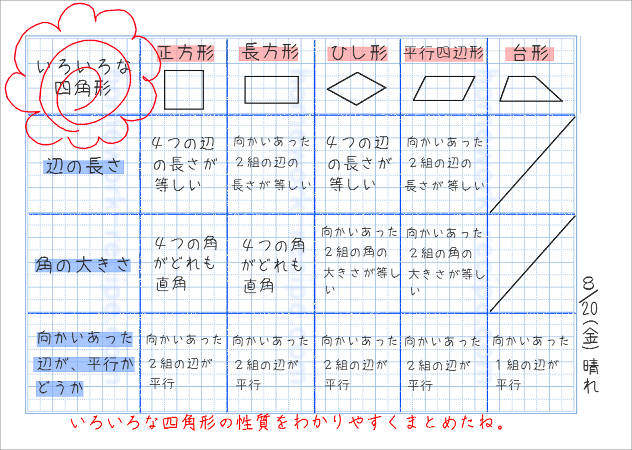



いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ



Http Pdf Drills App Com Images 864 Original Pdf




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su
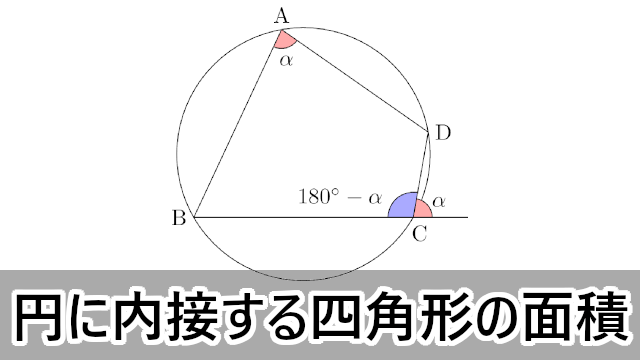



数学ia 円に内接する四角形の面積 大学入試数学の考え方と解法
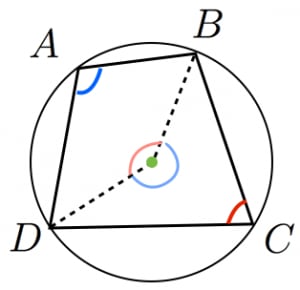



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語




中2数学 長方形の対角線 5分で学習 Youtube




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月



0 件のコメント:
コメントを投稿